| nextnano.com nextnano│ Download | Search | Copyright | Publications * password protected |
nextnano│ software
|
|
| Geometry objects region |
|
|
|
|
|
RegionsBasic geometry objectsTo built up a geometry, there are - dependent on the dimension of the
simulation to be performed - various basic geometry elements available. General specifiers
an integer number
an integer number
1-dimensional objects (only possible in 1D simulations):
2-dimensional objects (only possible in 2D simulations):
3-dimensional objects (only possible in 3D simulations):
Details of specification1-dimensional objectsLine
Chosen coordinates must be consistent with simulation orientation.
2-dimensional objectsRectangle
Two pairs of delimiting coordinates are required. Whether these have to be x-coordinates and y-coordinates as in the example above, or another combination (e.g. x, z) depends on the simulation orientation which is specified already.
Circle
The
Triangle (can also be specified using
|
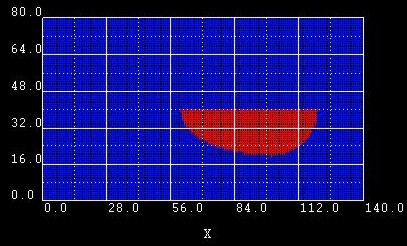 |
semi-ellipse-base = xmin xmax ymin ymax
Example 1:
From these data, the following points are extracted:
(point: |
|
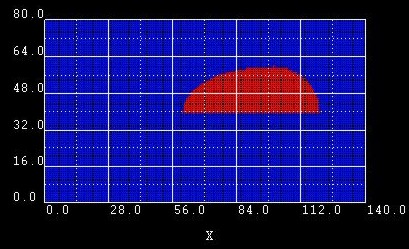 |
Example 2:
We changed the y1 coordinate of |
|
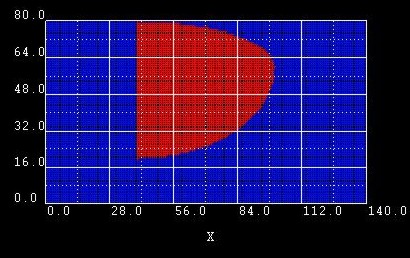 |
Example 3:
Here we changed |
|
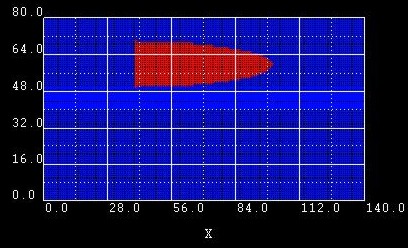 |
Example 4:
Here we changed the ymin and ymax coordinates of |
|
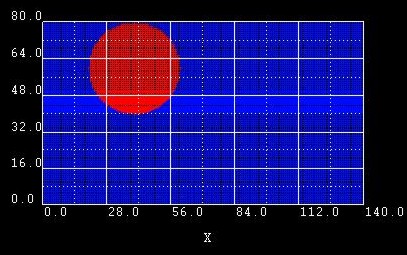 |
Example 5:
Here we built a circle out of 2 semi-ellipses. However, it is obviously
easier to use |
|
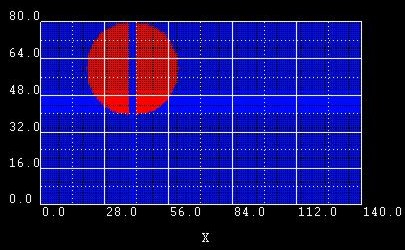 |
Example 6:
Same as example 5 but this time, we moved the baselines a little bit apart from each other to make example 5 easier to understand. |
$regions
region-number = 1
base-geometry = cuboid
region-priority = 1
x-coordinates = xmin xmax
y-coordinates = ymin ymax
z-coordinates = zmin zmax
$end_regions
The surfaces of the cuboid are assumed to be in coordinate planes of the
simulation coordinate system. The coordinates above specify the six coordinate
planes which limit the cuboid.
$regions
region-number = 1
base-geometry = sphere
region-priority = 1
center = x
y z ! [nm]
radius =
r
! [nm]
$end_regions
The sphere is defined by a center
with coordinates (x,y,z) and a radius r.
$regions
region-number = 1
base-geometry = obelisk
region-priority = 1
base-coordinates = xmin xmax ymin ymax zmin zmax
top-coordinates = xmin xmax ymin ymax zmin zmax
$end_regions
Base and top plane of the obelisk have to be in parallel coordinate planes.
These planes are identified by the implicit rule, that a pair of coordinate
values (e.g. ymin ymax) has the same value (ymin =
ymax).
In this example, the plane is in the (x,z)-coordinate
plane. The remaining four coordinates specify a rectangle in the corresponding
plane.
$regions
region-number = 1
base-geometry =
truncated-cone
! can be used to specify a cylinder
region-priority = 1
base-coordinates = xmin xmax ymin ymax zmin zmax
top-coordinates = xmin xmax ymin ymax zmin zmax
$end_regions
A cone with its apex cut off by a plane is called a truncated cone. In our implementation, the truncated cone is bounded by two ellipses of different size that are aligned parallel to each other.
Base and top plane of the truncated cone have to be in parallel coordinate planes. This
plane is identified by the implicit rule, that a pair of coordinate values (e.g.
xmin xmax) has the same value (xmin =
xmax). In this
example, the plane is in the (y,z)-coordinate plane.
ymin ymax and zmin
zmax specify the
diameter of the truncated cone top and base in the y and z direction, respectively. This
corresponds to the specification of ellipses in the base and top plane.
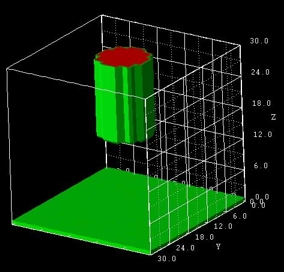
How to specify a cylinder?
A cylinder is specified as a special case of a
truncated-cone where the two boundary planes are circles.
For a truncated cone, one specifies base and top coordinates. Let us assume we have a
spherical cylinder of diameter 10 nm and height 15 nm. Then the base and top coordinates
would be, for example,
base-coordinates =
10.0 20.0 10.0 20.0 15.0 15.0
! (xmin,xmax,ymin,ymax,zmin,zmax) =
(10,20,10,20,15,15) top-coordinates = 10.0 20.0
10.0 20.0 30.0 30.0
! (xmin,xmax,ymin,ymax,zmin,zmax) =
(10,20,10,20,30,30)
$regions
region-number = 1
base-geometry = cone
region-priority = 1
base-coordinates = xmin xmax ymin ymax zmin zmax
top-coordinates = x y z
$end_regions
Base plane of the cone has to be in parallel to the coordinate system planes. This
plane is identified by the implicit rule, that a pair of coordinate values (e.g.
xmin xmax) has the same value (xmin =
xmax). In this
example, the plane is in the (y,z)-coordinate plane.
ymin ymax and zmin
zmax specify the
diameter of the cone base in the y and z direction, respectively. This
corresponds to the specification of an ellipse in the base plane. The top of the
cone, the apex, is defined by the point (x,y,z).
The cone does not have to be right circular (where circular
means that the base is a circle and right means that the axis passes
through the center of the base at right angles to its plane).
Oblique cones are allowed, in which the axis does not pass
perpendicularly through the center of the base.
The following figure shows several cones and truncated-cones
(including the special case of cylinders). The related input file is
called 3D_cone.in.

The cones are defined as follows:
!-------------------------------------------------------------------------------
! This is a cylinder. The base and top planes are parallel to the (y,z) plane.
!------------------------------------------------------------------------------
region-number = 1
base-geometry = truncated-cone
region-priority = 1 !
cylinder
base-coordinates = 80.0 80.0
-80.0 -60.0 -80.0 -60.0
! xmin xmax ymin ymax zmin zmax
top-coordinates = 40.0 40.0
-80.0 -60.0 -80.0 -60.0
! xmin xmax ymin ymax zmin zmax
!-------------------------------------------------------------------------------
! This is a right circular cone. The base plane is parallel to the (y,z) plane.
!-------------------------------------------------------------------------------
region-number = 2
base-geometry = cone
region-priority = 1 !
cone (right circular)
base-coordinates = -80.0 -80.0
50.0 90.0 50.0 90.0
! xmin xmax ymin ymax zmin zmax
top-coordinates = -10.0 70.0 70.0
! x y z
!--------------------------------------------------------------------------------------------------------
! This is a cone where the projection of the apex onto the base plane is located
outside the base plane.
! The base plane is parallel to the (y,z) plane.
!--------------------------------------------------------------------------------------------------------
region-number = 3
base-geometry = cone
region-priority = 2 !
cone
base-coordinates = -10.0 -10.0 -60.0
-20.0 -80.0 -20.0
! xmin xmax ymin ymax zmin zmax
top-coordinates = 40.0 -10.0 -10.0
! x y z
!--------------------------------------------------------------------------
! This is a truncated cone. The base plane is parallel to the (y,z) plane.
!--------------------------------------------------------------------------
region-number = 4
base-geometry = truncated-cone
region-priority = 3 !
truncated-cone
base-coordinates = 20.0 20.0
50.0 90.0 50.0 100.0
! xmin xmax ymin ymax zmin zmax
top-coordinates = 50.0 50.0
60.0 80.0 60.0 70.0
! xmin xmax ymin ymax zmin zmax
!--------------------------------------------------------------------------------------------------------------------
! These are three truncated cones where the projection of the top plane on the
base plane is outside the base plane.
! The base plane is parallel to the (y,z) plane.
!--------------------------------------------------------------------------------------------------------------------
region-number = 5
base-geometry = truncated-cone
region-priority = 4 !
truncated-cone
base-coordinates = -50.0 -50.0
20.0 40.0 20.0 60.0
! xmin xmax ymin ymax zmin zmax
top-coordinates = -20.0 -20.0
50.0 80.0 20.0 40.0
! xmin xmax ymin ymax zmin zmax
$regions
region-number = 1
base-geometry = semiellipsoid
region-priority = 1
base-coordinates = xmin xmax ymin ymax zmin zmax
top-coordinates = xtop ytop ztop
$end_regions
Base plane of the semiellipsoid must be in a coordinate plane. This plane is
identified by the implicit rule, that a pair of coordinate values (e.g.
ymin ymax) has identical values (ymin =
ymax).
In this example, the plane is in the (x,z)-coordinate plane. Top coordinates
specify an arbitrary point "above" the ellipse, representing the base of the
semiellipsoid.
Example: 3D sphere
A 3D sphere can be constructed from two semiellipsoids. However, it is
obviously easier to use
sphere instead.
In this example, the
bottom planes of the two half-spheres are at z = 5 nm.
The upper half-sphere extends from 5 nm to 6 nm, the lower half-sphere from 5 nm
to 4 nm.
The extensions in x and y directions for both half-spheres are from 4 nm to 6
nm.
Consequently, the sphere has a diameter of 2 nm.
region-number = 1(upper half-sphere)
base-geometry = semiellipsoid
!
base-coordinates = 4.0 6.0 4.0 6.0
5.0 5.0 ! xmin xmax ymin ymax zmin=zmax
top-coordinates = 5.0 5.0 6.0
! xtop ytop ztop
region-number = 2
base-geometry = semiellipsoid
!
base-coordinates = 4.0 6.0 4.0 6.0
5.0 5.0 ! xmin xmax ymin ymax zmin=zmax
top-coordinates = 5.0 5.0 4.0
! xtop ytop ztop

$regions
region-number = 1
base-geometry =
hexagonal-obelisk
region-priority = 1
base-coordinates = xmin xmax ymin ymax zmin zmax
top-coordinates = xmin xmax ymin ymax zmin zmax
$end_regions
Base and top plane of the hexagonal-obelisk have to be in parallel coordinate planes.
These planes are identified by the implicit rule, that a pair of coordinate
values (e.g. zmin
zmax) has the same value (zmin =
zmax).
In this example, the plane is in the (x,y)-coordinate
plane. The remaining four coordinates specify a rectangle in the corresponding
plane.
This geometry element is useful for wurtzite.
Many thanks to Lu Fu-Fa (Institute of Technology (CCIT), Taiwan, R.O.C.) for
useful suggestions regarding the implementation of this geometry element.
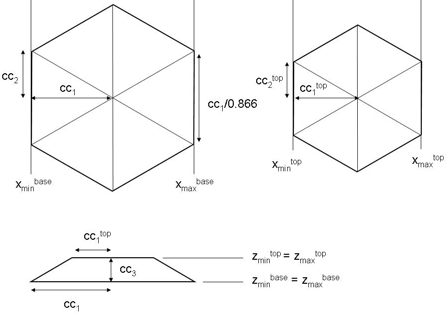
Two hexagonal-obelisk shapes are
possible:
zmin =
zmax).xmin(base) =
xmin(top)
xmax(base) =
xmax(top)
ymin(base) =
ymin(top)
ymax(base) =
ymax(top)
ymax(base)
-
ymin(base)
> (xmax(base)
-
xmin(base)) / 0.866 zmin =
zmax).xmin(top), xmax(top),
ymin(top), ymax(top)
arbitrary
ymax -
ymin > (xmax
-
xmin) / 0.866For both shapes it holds:
zmax(top)
- zmax(base)
(zmin =
zmax)
xmax(base) - xmin(base) ymax(base)
-
ymin(base)
> (xmax(base)
-
xmin(base)) / 0.866 is fullfilled:xmax(base)
- xmin(base)]/0.866 [Note:
0.866 = cos(30░)]
ymax(base) - ymin(base) > width along x if ymax(base)
-
ymin(base)
> xmax(base)
-
xmin(base)xmin(base)
+ xmax(base))ymin(base)
+ ymax(base)):
ymin(base) and ymax(base)
can be used to shift the hexagon along the y axis.Two sides of the hexagonal base plane are aligned parallel to the y axis.
To rotate the hexagonal base plane by 30 degrees, the user has to specify
values for
xmin(top), xmax(top),
ymin(top),
ymax(top) so that it holds:
xmax(top) -
xmin(top) > ymax(top)
- ymin(top)
In this case it holds:
xmax(base) -
xmin(base)
> (ymax(base)
-
ymin(base)) / 0.866 is fullfilled:ymax(base)
- ymin(base)]/0.866 [Note: 0.866 =
cos(30░)]
ymax(base) -
ymin(base) < width along x if
xmax(base) -
xmin(base)
> ymax(base)
- ymin(base)xmin(base)
+ xmax(base)):
xmin(base) and xmax(base)
can be used to shift the hexagon along the x axis.If the 6-fold rotational axis is oriented along the x (i.e.
xmin =
xmax) or y directions (i.e.
ymin =
ymax), cyclic permutations hold for
the above statements.
Example input file: 3DHexagonalObelisk.in
If you want to obtain this input file, please submit a support ticket.
Screenshots:
Hexagonal shaped pyramid with flat top plane:
 |
 |
 |
 |
Hexagonal shaped pyramid:
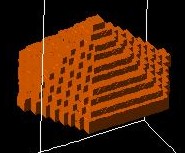  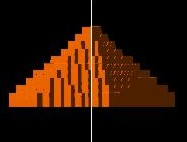 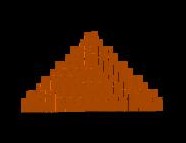 |
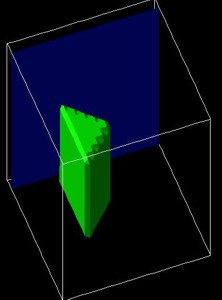
Hexagonal shaped "cylinder":
|
|
$regions
region-number = 1
base-geometry =
triangular-prism
region-priority = 1
corner-coordinates = x1 y1 z1 x2 y2
z2 x3 y3 z3
x4 y4
z4 x5 y5 z5 x6 y6 z6
$end_regions
Example:
corner-coordinates = 10.0 10.0 10.0
! x1 y1 z1
10.0 30.0 10.0 ! x2 y2 z2
20.0 20.0 10.0 ! x3 y3 z3
10.0 10.0 40.0 ! x4 y4 z4
10.0 30.0 40.0 ! x5 y5 z5
20.0 20.0 40.0 ! x6 y6 z6
Restrictions: triangular-prism
must be oriented so that the triangles are perpendicular to either the x, y
or z directions.
Example: Triangles perpendicular to z direction. Then it must hold:
==> corner-coordinates => z1 = z2 = z3In addition it holds:
z4 = z5 = z6
x1 = x4, y1 = y4
x2 = x5, y2 = y5
x3 = x6, y3 = y6
|
|