nextnano3 - Tutorial
next generation 3D nano device simulator
1D Tutorial
Two-dimensional electron gas in an AlGaN/GaN field effect transistor
Author: Stefan Birner
->
Jogai_AlGaNGaN_FET_JAP2003_noGaNcap_Fig4Fig1Fig7_1D_nn3.in -
input file for nextnano3 software
(also available as 2D input file)
->
Jogai_AlGaNGaN_FET_JAP2003_noGaNcap_Fig4Fig1Fig7_1D_nnp.in -
(also available as 2D input file)
->
Jogai_AlGaNGaN_FET_JAP2003_noGaNcap_Fig2Fig3_1D_nn3.in -
(also available as 2D input file)
->
Jogai_AlGaNGaN_FET_JAP2003_noGaNcap_Fig2Fig3_1D_nnp.in -
(also available as 2D input file)
->
Jogai_AlGaNGaN_FET_JAP2003_GaNcap_Fig4_1D_nn3.in -
(also available as 2D input file)
->
Jogai_AlGaNGaN_FET_JAP2003_GaNcap_Fig4_1D_nnp.in -
(also available as 2D input file)
->
Jogai_AlGaNGaN_FET_JAP2003_GaNcap_Fig6Fig5_1D_nn3.in -
(also available as 2D input file)
->
Jogai_AlGaNGaN_FET_JAP2003_GaNcap_Fig6Fig5_1D_nnp.in -
These input files are included in the latest version.
Two-dimensional electron gas in an AlGaN/GaN field effect transistor
This tutorial is based on:
[Jogai2003]
Influence of surface states on the two-dimensional electron gas in AlGaN/GaN
heterojunction field-effect transistors
B. Jogai
J. Appl. Phys. 93, 1631 (2003)
For this one-dimensional simulation of an AlGaN/GaN heterojunction field
effect transistor (HFET) we are solving self-consistently the
Schrödinger-Poisson equation taking into account strain, and piezo-
and pyroelectric charge densities.
- At the left boundary we use a Schottky contact boundary condition with a
Schottky barrier height of phiB = 1.4 eV.
Note that in Fig. 1 of [Jogai2003], the Schottky barrier height
corresponds to
e phiB = Ec - EF
which fixes the conduction band edge energy Ec above the Fermi energy EF.
e is the elementary charge.
Alternative boundary conditions such as
- a fixed surface charge density or
- surface states based on incomplete ionization of donor or acceptor states
are
described in the Schottky barrier
tutorial.
- Our simulated structure is undoped. Note that the 2DEG is present even in the
absence of doping due to piezo- and pyroelectric interface charge densities.
- The temperature is set to 300 K in all simulations.
- We only consider cation-faced structures, i.e. we have rotated
the crystal so that our [000-1] direction
points along the positive x direction.
The following figure shows the results of these input files:
==> 1DJogai_AlGaNGaN_FET_JAP2003_noGaNcap_Fig4Fig1Fig7_nn3.in -
input file for nextnano3 software
==> 1DJogai_AlGaNGaN_FET_JAP2003_noGaNcap_Fig4Fig1Fig7_nnp.in -
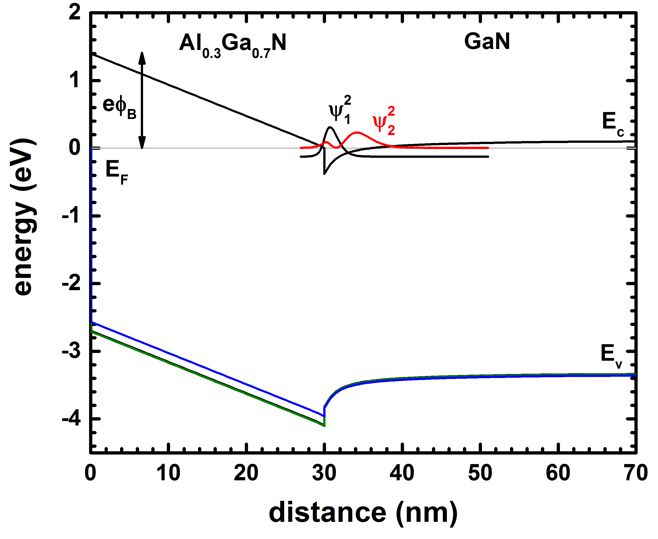
Shown are the conduction and three valence band edges together with the
probability densities of the two lowest subbands of a 30 nm Al0.3Ga0.7N
/ 40 nm GaN heterostructure.
Variation of the AlxGa1-xN layer thickness and alloy content
x (Fig. 2 and Fig. 3 of [Jogai2003])
==> Jogai_AlGaNGaN_FET_JAP2003_noGaNcap_Fig2Fig3_1D_nn3.in - input file for nextnano3 software
==> Jogai_AlGaNGaN_FET_JAP2003_noGaNcap_Fig2Fig3_1D_nnp.in - input file for nextnano++ software
Now we try to reproduce Fig. 2 and Fig. 3 of [Jogai2003].
We are calculating the variation of the 2DEG density with the
- AlxGa1-xN layer thickness and
- mole fraction (alloy content x).
Within the nextnano3 input file, we can perform a sweep
over the alloy concentration very conveniently:
%AlloySweepActive = yes
! sweep alloy concentration from 0.4 to 0.0
(HighlightInUserInterface)
The thickness of the AlxGa1-xN barrier is defined
as a variable.
%ThicknessAlGaN = 30.0
! thickness of AlGaN spacer
(ListOfValues:6,10,14,18,22,26,30,34,38)(DisplayUnit:nm)(HighlightInUserInterface)
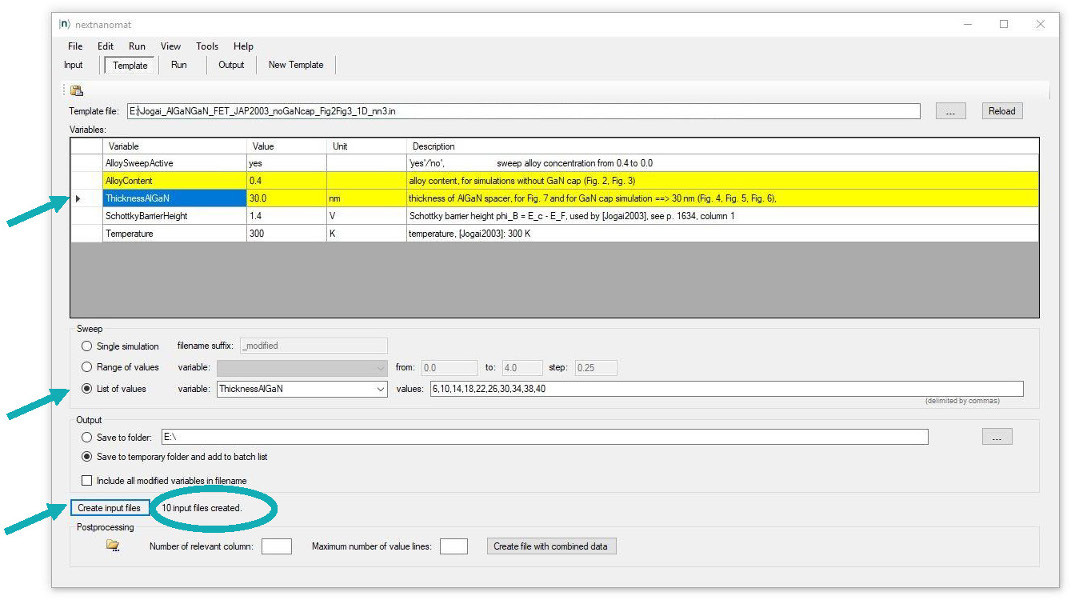
The input files are created automatically and are added to the "Run" tab.
The 2DEG sheet carrier concentration can be found in this file:
densities/int_el_dens1D.dat
This file contains the integrated electron density for each region
cluster.
In our case, the total electron density is relevant which is the sum of cluster
#3 (AlGaN barrier) and cluster #4 (GaN well) because the quantum cluster extends
over these two clusters.
The first column contains the sweep index which is the alloy content.
sweep_index Cl_1[1/cm^2]
Cl_2[1/cm^2] Cl_3[1/cm^2] Cl_4[1/cm^2]
Cl_5[1/cm^2] Cl_6[1/cm^2] Total[1/cm^2]
0.400000E+00 0.231809E-02
0.798938E+08 0.534667E+12 0.983171E+13 0.133962E+12
0.000000E+00 0.105004E+14
...
The following figure shows the total integrated electron density (Total[1/cm^2])
as a function of alloy concentration for various AlGaN thicknesses.
Note that these results were obtained by using one input file
template only: 1DJogai_AlGaNGaN_FET_JAP2003_nn3_Fig2Fig3.in
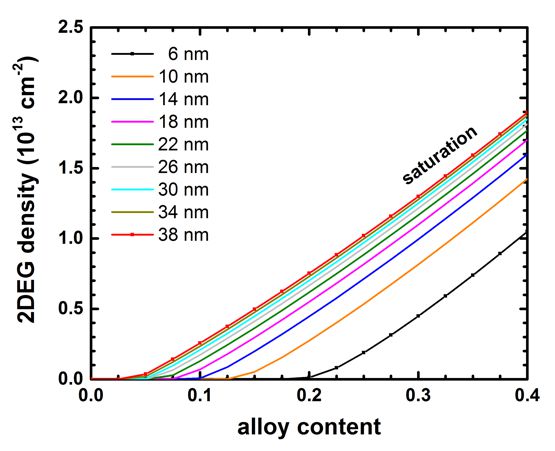
For a given barrier thickness, the 2DEG sheet carrier concentration varies
almost linearly with alloy concentration x.
The 2DEG density approaches saturation as the barrier thickness is increased.
This fact can be better seen in the next plot where we show exactly the same
data.
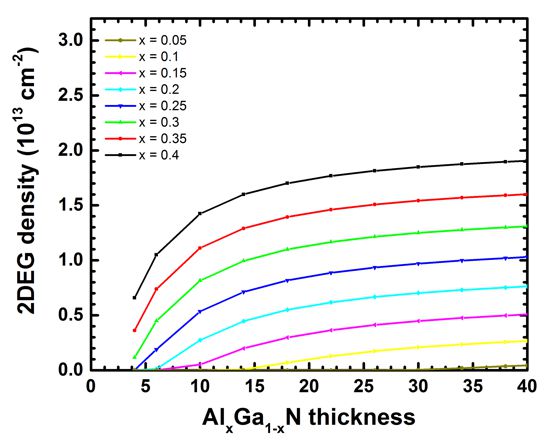
Our results seem to be in reasonable agreement to the simulations of [Jogai2003]
(Fig. 2 and Fig. 3).
Variation of the Schottky barrier height (Fig. 7 of [Jogai2003])
==> Jogai_AlGaNGaN_FET_JAP2003_noGaNcap_Fig4Fig1Fig7_1D_nn3.in - input file for nextnano3 software
==> Jogai_AlGaNGaN_FET_JAP2003_noGaNcap_Fig4Fig1Fig7_1D_nnp.in -
Now we vary the Schottky barrier height phiB and calculate
for each value the 2DEG density.
%SchottkyBarrierHeight = 1.4
! Schottky barrier height phi_B = E_c - E_F, used by
[Jogai2003], see p. 1634, column 1
(ListOfValues:1.40,1.42,1.65)(RangeOfValues:From=0.0,To=4.0,Step=0.25)(DisplayUnit:V)
This situation is equivalent to fixing the surface potential to
e phiB = Ec - EF.
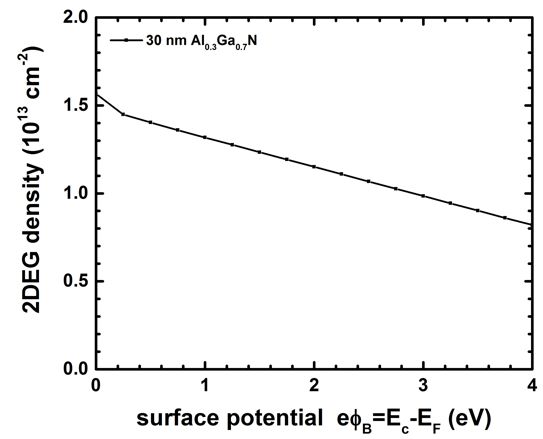
The following figure shows the calculated 2DEG density as a function of
Schottky barrier height, i.e. surface potential.
We used a 30 nm Al0.3Ga0.7N barrier.
Again, the 2DEG sheet carrier concentration can be found in this file:
densities/int_el_dens1D.dat (Total[1/cm^2])
The results are in reasonable agreement to Fig. 7 of [Jogai2003].
AlGaN/GaN FET including a GaN cap layer
==> Jogai_AlGaNGaN_FET_JAP2003_GaNcap_Fig4_1D_nn3.in - input file for nextnano3 software
==> Jogai_AlGaNGaN_FET_JAP2003_GaNcap_Fig4_1D_nnp.in -
==> Jogai_AlGaNGaN_FET_JAP2003_noGaNcap_Fig4Fig1Fig7_1D_nn3.in -
==> Jogai_AlGaNGaN_FET_JAP2003_noGaNcap_Fig4Fig1Fig7_1D_nnp.in -
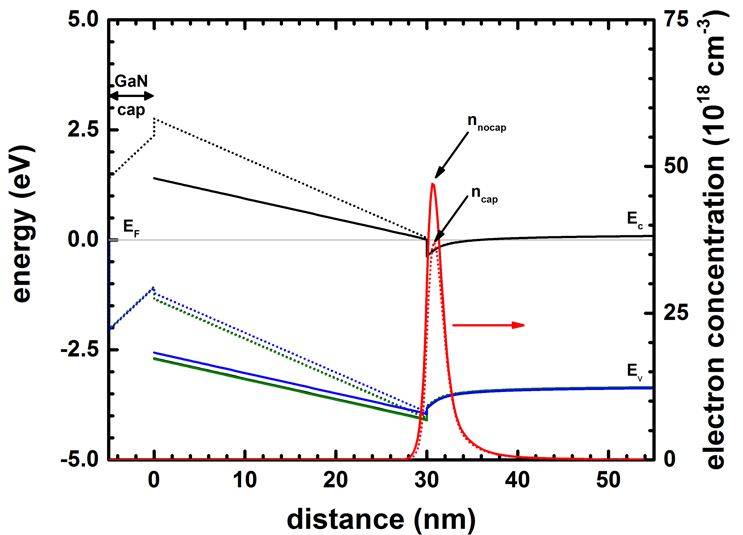
Now we compare HFET structures with and without a GaN cap layer.
GaN-capped
HFETs have a lower 2DEG density compared to uncapped structures.
When introducing a GaN cap layer, the density of the 2DEG is reduced.
- 5 nm cap, 30 nm Al0.3Ga0.7N barrier. The
calculated 2DEG density is n = 1.03 * 1013 cm-2 (n = 1.20 * 1013 cm-2
[Jogai2003]).
- without cap, 30 nm Al0.3Ga0.7N barrier. The
calculated 2DEG density is n = 1.25 * 1013 cm-2 (n = 1.47 * 1013 cm-2
[Jogai2003]).
The following figure shows the conduction and valence band edges of an Al0.3Ga0.7N/GaN
FET with (solid lines) and without (dotted lines) a 5 nm GaN cap layer.
==> Jogai_AlGaNGaN_FET_JAP2003_GaNcap_Fig6Fig5_1D_nn3.in - input file for nextnano3 software
==> Jogai_AlGaNGaN_FET_JAP2003_GaNcap_Fig6Fig5_1D_nnp.in -
The following figure shows the band edges and the electron and hole densities
for a 14 nm GaN cap layer.
The Al0.3Ga0.7N barrier thickness is 30 nm.
For GaN cap layers thicker than 14 nm, a 2DHG forms.
The density of the 2DHG screens the surface potential so that the density of the
2DEG is maintained at a constant level even if the GaN cap layer thickness
increases further.
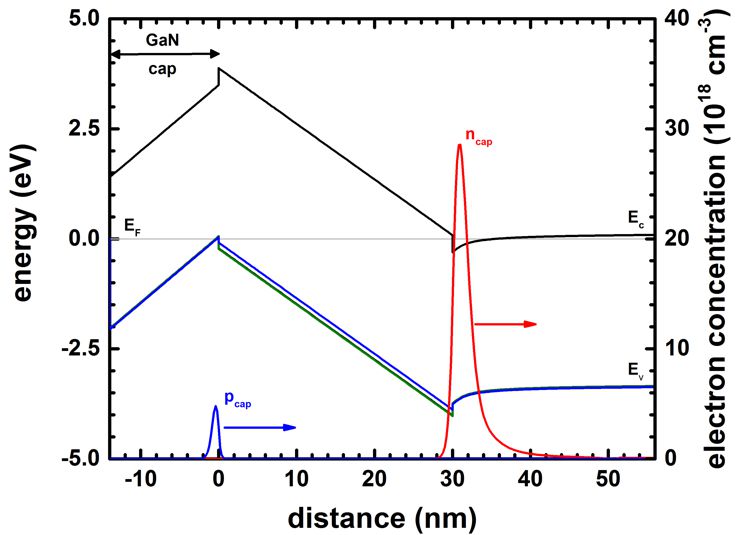
The calculated 2DHG density is p = 0.513 * 1012 cm-2 (p = 1.77 * 1012 cm-2
[Jogai2003]).
The calculated 2DEG density is n = 0.839 * 1013 cm-2 (n = 1.009 * 1013 cm-2
[Jogai2003]).
Variation of the GaN cap layer thickness (Fig. 5 of [Jogai2003])
==> Jogai_AlGaNGaN_FET_JAP2003_GaNcap_Fig6Fig5_1D_nn3.in - input file for nextnano3 software
==> Jogai_AlGaNGaN_FET_JAP2003_GaNcap_Fig6Fig5_1D_nnp.in -
Now we are going to vary the GaN cap layer thickness.
%ThicknessGaNcap = 5.0
! thickness of GaN cap layer for GaN cap simulation (Fig.
4, Fig. 5),
(ListOfValues:1,2,3,4,5,7,9,11,12,13,14,15,17,20,25,30)(DisplayUnit:nm)(HighlightInUserInterface)
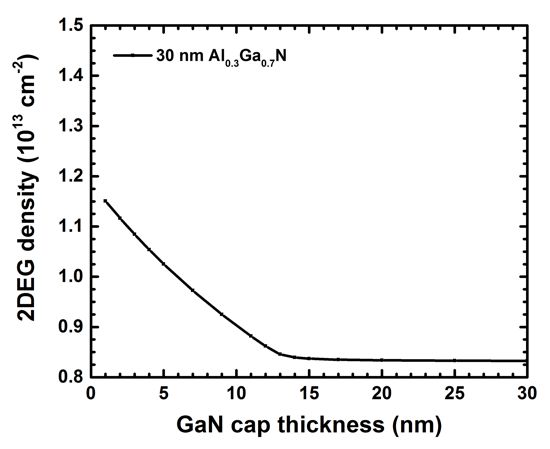
The following figure shows the 2DEG density vs. GaN cap layer thickness for a 30 nm Al0.3Ga0.7N
barrier.
Beyond a GaN cap layer thickness of ~13 nm (12 nm [Jogai2003])
the 2DEG density saturates.
Additional comments
In contrast to the article of [Jogai2003], we did not include
exchange-correlation effects. (To do: Add to this tutorial.)
In contrast to the article of [Jogai2003], we used a
single-band model for the 2DHG rather than a 6-band k.p model.
(To do: Add 6-band k.p for the holes to this tutorial.)
|