nextnano³ - Tutorial

next generation 3D nano device simulator

1D Tutorial

InAs / GaSb broken gap quantum well (BGQW) (type-II band alignment)

Author: Stefan Birner

-> 1DInAs_GaSb_BGQW_k_zero_nn3.in       / *_nnp.in                  - input file for the nextnano³ and nextnano++ software
-> 1DInAs_GaSb_BGQW_k_parallel_nn3.in   / *_nnp_01.in / *_nnp_11.in - input file for the nextnano³ and nextnano++ software

These input files are included in the latest version.

InAs / GaSb broken gap quantum well (BGQW) (type-II band alignment)

This tutorial aims to reproduce Figs. 1, 2(a), 2(b) and 3 of

Hybridization of electron, light-hole, and heavy-hole states in InAs/GaSb quantum wells
A. Zakharova, S.T. Yen, K.A. Chao
Physical Review B 64, 235332 (2001)

The material parameters were taken from

Optical transitions in broken gap heterostructures
E. Halvorsen, Y. Galperin, K.A. Chao
Physical Review B 61 (24), 16743 (2000)

The heterostructure is a broken gap quantum well (BGQW) with 15 nm InAs and 10 nm GaSb, sandwiched between two 10 nm AlSb layers.
Note that this heterostructure is asymmetric.

To be consistent with the above cited papers, strain is not included into the calculations although this would be possible.

The structure has a type-II band alignment, i.e. the electrons are confined in the InAs layer, whereas the holes are confined in the GaSb layer.

Depending on the width of the InAs and/or GaSb layers, things can be even more complicated because the hole states can hybridize with the electron states, making it difficult to distinguish between electron-like and hole-like states.

Another difficulty arises because the lowest electron states might be located below the highest hole states. This requires a new algorithm to occupy the states according to a suitable Fermi level.

The following figure shows the electron and hole band edges of the BGQW structure.
- band_structure/cb1D_001.dat (Gamma  conduction band edge) in units of [eV]
- band_structure/vb1D_001.dat (heavy   hole valence band edge) in units of [eV]
- band_structure/vb1D_002.dat (light     hole valence band edge) in units of [eV]
- band_structure/vb1D_003.dat (split-off hole valence band edge) in units of [eV]



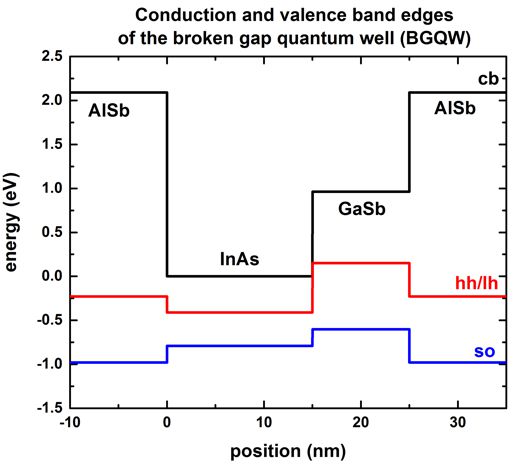
The origin of the energy scale is set to the InAs conduction band edge energy. The heavy hole and light hole band edges are degenerate because we neglect the effects of strain to be consistent with the above cited papers.

Results

• -> 1DInAs_GaSb_BGQW_k_zero.in
  
  The following figure shows the conduction band edge and the heavy/light hole valence band edges in this BGQW structure
  together with the electron (e1, e2), heavy hole (hh1, hh2, hh3) and light hole (lh1) energies and wave functions (psi²), calculated within 8-band k.p theory at the zone center, i.e. at k_|| = 0.
  
  One can clearly see that the electron state (e1, e2) are confined in the InAs layer (left part of the figure),
  whereas the heavy (hh1, hh2, hh3) and light hole (lh1) states are confined in the GaSb layer (right part of the figure).
  One can see a slight hybridization of the e1 and lh1 states, i.e. these states are mixed states whereas the heavy hole states (hh1, hh2, hh3) are not mixed and thus confined in the GaSb layer.
  
  - Schroedinger_kp/kp_8x8psi_squared_qc001_el_kpar0001_1D_dir.dat       - contains Psi_i²
- Schroedinger_kp/kp_8x8psi_squared_qc001_el_kpar0001_1D_dir_shift.dat - contains Psi_i² + E_i
  
  The latter file contains the square of the wave functions (for kpar0001, i.e k_|| = 0, i.e. k_x = k_y = 0), shifted by their energies, so that one can nicely plot the conduction and valence band edges together with the square of the wave functions.
  
  
  
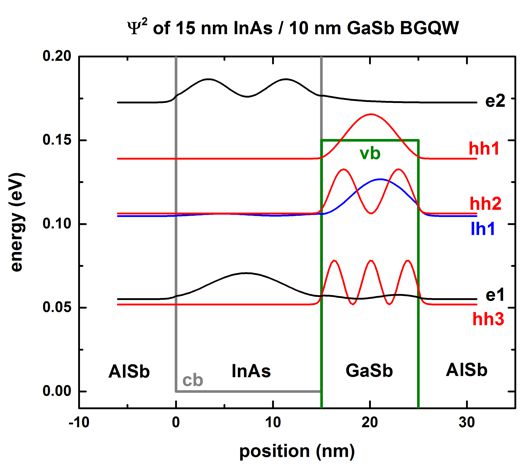
  The energies of the eigenstates are in units of [eV] and are contained in this file:
  - Schroedinger_kp/kp_8x8eigenvalues_qc001_el_kpar0001_1D_dir.dat.dat
   
• -> 1DInAs_GaSb_BGQW_k_parallel.in

  The following figure shows the E(k_||) dispersion of the electron and hole states along the [10] direction and along the [11] direction in (k_x,k_y) space.
  The [01] direction has the same dispersion due to symmetry arguments.
  
  In this input file, the energy levels and wave functions for 24 k_|| points along a line from (k_x,k_y) = (0,0) to (k_x,k_y) = (0,k_y) have been calculated.
  
  - Schroedinger_kp/kpar1D_disp_01_00el_8x8kp_ev_min001_ev_max020.dat
  contains the k_|| dispersion from [00] to [01] because in the input file it is specifed:
  
    $output-kp-data
     !k-par-dispersion = 01-00      ! plot k_|| dispersion from [00] to [01]
      k-par-dispersion = 01-00-11   ! plot k_|| dispersion from [01] to [00] to [11]

  The first column contains the k_|| value, the other columns contain the eigenvalues for each k_|| value: E_n(k_||) = E_n(k_x,k_y) =  E_n(0,k_y)
  Here, n = 1,...,20.   (...ev_min001_ev_max020...)
  Note that for this particular example, the eigenvalues have to be sorted manually if you want to connect the energy values,
    i.e. to include lines ("lines are a guide to the eye").

  The black lines are the results of the nextnano++ software, the red dots are the results of the nextnano³ software.
  
  
  
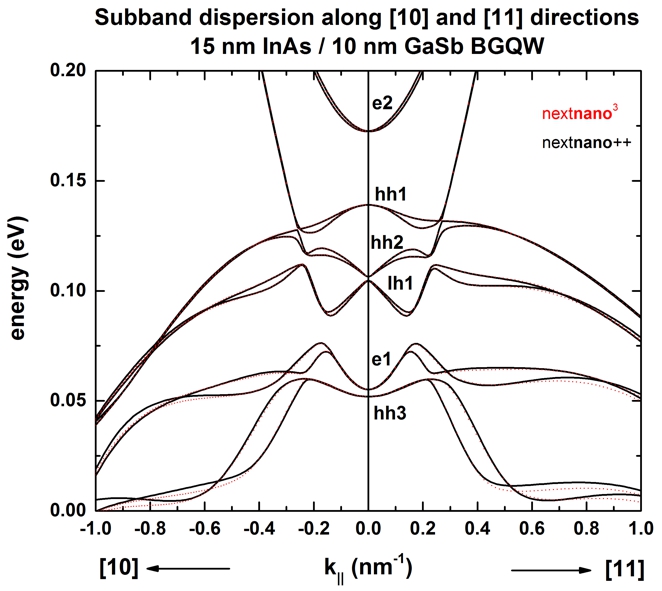
  At an in-plane wave vector of 0.014 1/Angstrom, strong intermixing between the e1 and the lh1 states occurs.
  In contrast to the wave functions at k_|| = 0, where the e1 and lh1 wave functions are nearly purely electron- or hole like, the wave functions at k_|| = (0,0.014)  = (0.014,0) are a mixture of electron and light hole wave functions. Compare with Fig. 4 of the A. Zakharova et al.
  
  In asymmetric quantum wells, the double spin degeneracy is lifted at finite values of k_|| because of spin-orbit interaction. This is the reason why we have two different dispersions E(k_||) for "spin up" and "spin down" states.
  This also means that the wave functions at finite k_|| are different for "spin up" and "spin down" states.
   
• The file
  Schroedinger_kp/kp_8x8k_parallel_qc001_el1D_dir.dat
  tells us which number of k_|| vector corresponds to (k_x,k_y).
  
     k_par_number   k_x [1/nm]      k_y [1/nm]
     1            0.000000E+000   0.000000E+000     ==>   k_|| = (k_x,k_y) = (0,0) [1/nm]
     ...
     29           0.000000E+000   1.400000E+000     ==>   k_|| = (k_x,k_y) = (0,0.14) [1/nm]
   1326           1.00000E+000    1.000000E+000     ==>   k_|| = (k_x,k_y) = (1.0,1.0) [1/nm]

 
• In the following figure, we plot the square of the wave functions for k_|| = (0,0.14) nm^-1.
  The corresponding label of our k_|| numbering is 29. Note that this labeling depends on the k_|| space resolution, i.e. the number of k_|| points that have been specified in the input file: num-kp-parallel = 10000
  
  The wave functions are contained in this file:
  - Schroedinger_kp/kp_8x8psi_squared_qc001_hl_kpar00029_1D_dir_shift.dat - contains Psi_i² + E_i
  
  
  
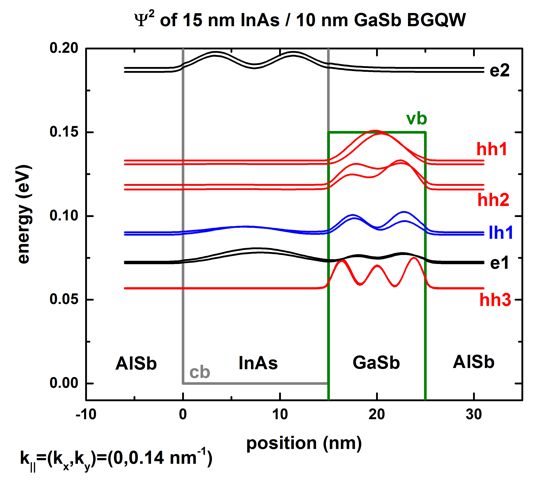
  The electron states (e1) couple strongly with the light hole states (lh1). This is expected from the energy dispersion plot because at 0.14 nm^-1 a strong anticrossing is present for these states.
  One can also clearly see that for spin up and spin down states, different energy levels and different probability densities exist.
  This is in contrast to the states at k_|| = 0 which are two-fold spin degenerate as shown in the figure further above.
  Our results are similar to Fig. 4 of Zakharova's paper.